Kuntavaalit 2025: Miltä näyttää Turku, kun minua ei enää ole?

Politiikassa katsotaan usein hyvin lyhyesti eteenpäin ja hyvin kapeasti sivuille: luvataan sitä, mikä on minulle itselleni ja minun äänestäjilleni tärkeintä juuri tänä vuonna. Aikajana voi toki olla pidempikin, mutta oma napa edellä mennään. Olen ehdolla Turussa vuoden 2025 kuntavaaleissa, ja ajattelin ottaa mahdollisimman päinvastaisen lähtökohdan. Elinaikalaskurin mukaan todennäköisin kuolinpäiväni on tällä hetkellä marraskuussa 2052. Minua kiinnostaakin eniten se, miltä Turku näyttää vuonna 2055, kun en todennäköisimmin ole sitä enää itse näkemässä.

Se ei tarkoita että lällyisin jossakin abstraktissa epätodellisuudessa. Tuossa vaiheessa omat lapseni ovat keski-ikäisiä, ja mahdolliset seuraavat sukupolvetkin ainakin aikuistumassa. Heille tätä tehdään, ja tämä lähestymistapa pakottaa tosissaan miettimään mitä konkreettisesti pitää tehdä juuri nyt. 

Kukaan ei vielä pysty ennustamaan kuinka pitkälle ilmastokriisi on edennyt vuonna 2055, mutta levottomuuksien alkutahteja varmasti nähdään. Sellaisessakaan tilanteessa ei pidä lamaantua, vaan tehdä se mitä tehtävissä on. Turku pärjää jotenkuten uudenlaisessakin maailmassa jos sopeutuminen aloitetaan nyt: sielläkin

        • liikutaan, mutta ympäristöystävällisesti (massiivinen panostus joukkoliikenteeseen), 
        • koitetaan kestää rankkasateita (infra kuntoon ja hulevedet hallintaan), 
        • halutaan kosketus lähiluontoon (viheralueet ja kaupunkipuistot kunniaan), 
        • yritetään pysyä terveinä (kaupunki voi ennaltaehkäistä paljon, esimerkiksi liikunnan kautta)
        • yritetään pysyä järjissään (sama kuin yllä, plus vaikkapa kulttuuri ja lähiluonto)
        • ollaan paljon nykyistä kansainvälisempiä (kotoutus kuntoon)
        • kannustetaan lapsia sivistymään ja oppimaan (koulut kunniaan)
        • tutkitaan, miten uusista kriiseistä selvitään (korkeakoulut)
        • innovoidaan uusia ratkaisuja uusiin kriiseihin (yritysten hyvinvoinnin varmistaminen)

Ihan perinteisiä Vihreitä asioita siis. Olin hieman hämmentynyt, kun huomasin, miten vähän tuo perspektiivin muuttaminen oman kuolemani jälkeisesti oikeastaan tuo mitään uutta poliittisiin näkemyksiini. Vihreät on jo nyt puolueista ainoa, joka oikeasti suunnittelee asioita yli monen sukupolven. Sillä linjalla kun jatketaan, hyviä asioita tapahtuu.

Jos ajatukseni resonoivat, ensisijaisesti toivon että pohtisit, voisitko itsekin olla näissä vaaleissa ehdolla. Vaalit voitetaan hyvillä ehdokaslistoilla, ja Turussakin listalla on edelleen tilaa. Toissijaisesti toivon, että lähtisit mukaan tekemään Vihreiden yhteistä kampanjaa, tai tarjoudut jonkun hyvän ehdokkaan kampanjapäälliköksi tai tukitiimiin. Vihreillä ei ole rahaa, mutta tiimityöllä olemme saaneet nollaresursseillakin paljon aikaan.

Kolmoissijaisesti: vaikka aika iso osa energiastani tuleekin menemään yhteiskampanjan luotsaamiseen ja muiden ehdokkaiden tsemppaamiseen (olen vetovastuussa koko Turun kampanjasta yhdessä loistavan Inari Harjuniemen kanssa), kasaan itsellenikin tukitiimin kampanjaani jos kiinnostuneita löytyy. Tervetuloa!

 

Mikä on poliitikon puoliintumisaika?

Politiikka polttaa nopeasti loppuun.  On yksittäisiä työn sankareita joiden ura kunnanvaltuustossa jatkuu neljällä tai viidellä eri vuosikymmenellä, mutta he ovat kuitenkin poikkeuksia. Varsinkin vähemmän näkyvillä paikoilla ihmisten vaihtuvuus on suurta.

Dataihminen kysyy heti: kuinka suurta? Poliitikon uran voi mallintaa radioaktiivisena prosessina: kenen tahansa pää voi hajota koska tahansa. Laajemmalle poliitikkojoukolle voidaan laskea puoliintumisaika, eli  aika jonka jälkeen puolet väestä on vaihtunut.

Datan löytäminen tähän analyysiin ei ole itsestäänselvyys, koska esimerkiksi puolueen jäsenyys on tiukasti salainen tieto. Avoimen ja julkisen datan puolelta löytyy kuitenkin pienikokoinen kultakaivos:  oikeusministeriön tulospalvelu, jossa on erittäin hyvin organisoitua vaalidataa vuodesta 2011 (ja vähemmän organisoitua vuodesta 2003). Vaalitulokset, samoin kuin ehdokkuudet vaaleissa, ovat julkista tietoa.

Eduskuntavaalien listoja tarkistelemalla ei voi tehdä juuri mitään johtopäätöksiä koko puolueen aktiiveista, koska niihin ehdokkaiksi valikoituu erittäin pieni määrä poikkeusyksilöitä.  Kuntavaaleissa sen sijaan ehdokaslista heijastaa paljon paremmin koko kenttää. Vaikka kuntavaalipaikoistakin on kilpailua, paikkoja on niin paljon, että varsin suuri osa minkä tahansa puolueen sen hetkisistä aktiiveista saa pelätä päätyvänsä ehdolle.

Siksi juuri kuntavaalidatasta voisi löytyä mielenkiintoinen läpileikkaus puolueen aktiiveista laajemminkin. Tulospalvelusta saa suoraan kaksi tietoa vuosien 2017 ja 2021 kuntavaaleista: ehdokkaan ikä vaalipäivänä, ja uudemmista vaaleista tieto siitä, onko hän ollut aiemmin ehdolla vastaavassa vaalissa.   Koodit ja käytetyt raakadatat löytyvät Githubistani.

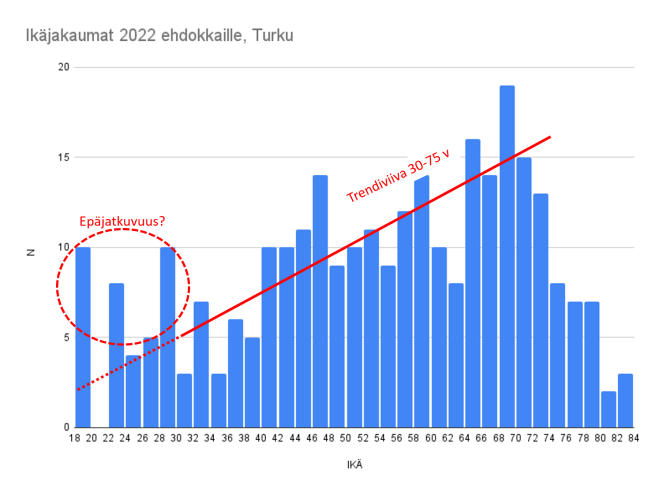
Ikäjakaumat

Ikä on mielenkiintoinen kysymys. Keskimääräinen kuntavaaliehdokas Suomessa on 50-vuotias. SDP:llä keski-ikä on hieman korkeampi, noin 53 vuotta. Vihreät poikkeavat muista erityisen dramaattisesti noin 43 vuoden keski-iällä.

Erot näkyvät erityisen selkeästi, kun tulokset piirretään tiheysfunktioina. SDP:n ja Vasemmistoliiton ikääntyneisyys näkyy hyvin. Vihreät poikkeavat profiililtaan selkeästi muista.

Tarkastelua voidaan tehdä myös kunnittain, laskien listojen keski-iät.  Vihreiden  poikkeavuus  on  tällöin  erityisen  selvä.

Kokemuksen jakaumat

Vaihtuvuus kuntavaaleissa on mielenkiintoisin muuttuja. Nyrkkisääntönä voidaan ajatella, että noin 50% vaihtuvuus kuntavaalien välillä olisi ihanteellinen. Silloin listoilla on sekä kokemusta että uudistumista. Käytännössä se tarkoittaisi noin neljän vuoden puoliintumisaikaa ehdokkaille.

Puolueiden välillä näkyy tässä suhteessa varsin merkittäviä eroja. Useimmilla puolueilla kokeneiden osuus on keskimäärin hieman yli 50%, SDP:llä jopa 63%. Kaksi puoluetta (Vihreät ja PS) erottuvat näistä selvästi noin 40% osuudellaan.

Näistä luvuista saadaan laskettua karkea puoliintumisaika. Oletetaan, että lista hajoaa eksponentiaalisesti aikavakiolla k: y=y0*exp(-k*t).   Jos neljän vuoden jälkeen listalla  on jäljellä  p poliitikkoa, puoliintumisaika saadaan kaavasta  t2=4*log(0.5)/log(p).

Nähdään, että keskimääräinen puoliintumisaika on noin 4.5 vuotta.  Vihreillä ja perussuomalaisilla puoliintumisaika on lyhyin, noin kolme vuotta. Kaikilla muilla puoliintumisaika on yli 4 vuotta, eli voidaan tulkita että keskimääräinen ehdokas säilyy aktiivisena hieman yli vaalikauden.  SDP:llä puoliintumisaika on kaikkein pisin, lähes tuplasti Vihreiden ja PS:n.

Kokemuksen ja iän korrelaatio

Mielenkiintoinen kuvaaja saadaan, jos piirretään puolueittain  kokeneiden osuus  ja  listan  keski-ikä.   Jos  kuvaaja nousee tasaisesti, voidaan tulkita että ikä tuo kokemusta: puolueella  on  aktiiveja,  jotka ovat monissa vaaleissa ehdolla.

Vihreät ovat käytännössä ainoa poikkeus tästä.  Vaikka PS:n ehdokkailla on keskimäärin vähän kokemusta,  ikääntyneemmillä listoilla on kuitenkin  kokemusta keskimäärin enemmän. Vihreiden listoilla taas kokemusta on lähes saman verran riippumatta siitä, mikä on listan keski-ikä.

Johtopäätökset

Keskimääräinen Vihreä kuntavaaliehdokas on nelikymppinen, ja puoliintuu kolmessa vuodessa — eli  kyllästyy ennen kuin ehtii edes toisiin kuntavaaleihinsa. Muiden puolueiden ehdokkaat ovat keskimäärin viisikymppisiä, ja heistä (pienehkö) enemmistö jatkaa harrastusta seuraavallakin vaalikaudella, puoliintuen 4-6 vuodessa (poikkeuksena ainoastaan perussuomalaiset).

Mielestäni on yksikäsitteisesti hyvä asia, että Vihreissä on paljon nuoria, ja että itsekin olen jo ikämiessarjassa.   Ei ole mitenkään toivottavaa, että sama pieni kaaderisto olisi vallankahvassa vuosikymmenestä toiseen.

Sen sijaan kokemuksen katoaminen on asia, jolla annetaan muille  tasoitusta.  Jos puolet väestä vaihtuu kolmen vuoden välein, jatkuvuutta ja pitkäjänteisyyttä on vaikea ylläpitää.  Olen itse ollut vastuuasemissa kaikissa Varsinais-Suomen Vihreissä vaaleissa vuoden 2020 jälkeen, ja  huomannut sitä kautta tämän vaihtuvuuden varjopuolet käytännön työssä. Kokeneiden toimijoiden uudelleeninnostaminen olisikin yksi selkeä kehityskohde seuraaville vuosille.

Kirjoittaja on ollut aktiivinen Vihreissä jo muutaman puoliintumisajan verran, ja pohtii jo vuosien 2024-2027 vaaleja.

Data ja nuoriso

Nuorissa on tulevaisuus. Tämä ei ole klisee, vaan fakta — ja fakta, jonka pitäisi olla erityisesti kirkon päättäjien mielessä koko ajan. Kirkko on lähes ainoa instituutio, joka katselee asioita satojen tai miksei tuhansienkin vuosien aikaskaalassa. Siinä skaalassa ei riitä ajatella, mitä juuri nyt tapahtuu, vaan on mietittävä myös sitä, mitä tapahtuu kun nykyinen miespolvi vaipuu unholaan.

Teksti julkaistu Turun Vihreän Kirkon blogissa 4.11.2022.

Itse nostin nuoret vaalikoneessa tärkeimmäksi painopisteeksi. Jos meillä ei ole aktiivisia ja kiinnostuneita nuoria toiminnassa lähivuosina, meillä ei 50 vuoden kuluttua ole toiminnassa ketään. Hyvin tiedetään, että nuorten aktiivisuus ja ylipäätään kirkkoon kuuluminen on suuri kysymysmerkki.  Jos on kiinnostunut kirkon jatkuvuudesta, tämän pitäisi herättää.

Dataihminen pyrkii tässä kohtaa löytämään numeroita, jotka kertovat tarinaa siitä, mihin täsmälleen pitäisi herätä. Kirkontilastot-fi-sivulla on mm ennusteita kirkon ja eri seurakuntien jäsenmääristä. Ennusteissa tehdään normaalit demografiset oletukset, eli käytännössä oletetaan että mikään ei radikaalisti muutu. Vaikka todellisessa elämässä asiat saattavatkin radikaalisti muuttua, nämä ennusteet ovat hyvä lähtökohta.

Turun ja Kaarinan seurakuntayhtymä on järkevä kokonaisuus, jonka ennustettavuus voi olla ainakin kohtalainen. Normaalein demografisin oletuksin kirkon jäsenmäärän kehitys Turussa ikäryhmittäin olisi alla olevan kaltainen. Silmiinpistävää kuvaajassa on erityisesti 20-29-vuotiaiden jäsenten a) suuri määrä ja b) voimakas hiipuminen. Turku on opiskelijakaupunki, ja opiskelijoiden trendit näkyvät täällä vahvasti. Kirkkoon kuuluminen ei ole opiskelijatrendi.

Kaikkein nuorimpien ikäluokkien osalta tämä kuvaaja saattaa olla ylioptimistinenkin. Jos vanhemmat eivät kuulu kirkkoon, on vaikea nähdä miksi syntyvät lapsetkaan kastettaisiin. Laskevaa trendiä näkyy kyllä nuorimmissa ikäluokissakin, mutta se voi todellisuudessa olla paljon jyrkempikin.

Varsinainen datatarina syntyy, jos mietitään ketä missäkin ikäryhmässä oikeasti on. Alla on noin 20 vuoden kehitys ikäryhmittäin. Esitystavan etuna on se, että mustia viivoja seuraamalla voi arvioida myös se, ketä nykyisiä ihmisiä missäkin ikäryhmässä on. Oma 50+ sukupolveni on 2040-luvulla 70+ sukupolvi, ja niin edelleen.

Toisin sanottuna: noin 40% turkulaisista kirkon jäsenistä kuuluu tällä hetkellä siihen yli 50-vuotiaiden ikäluokkaan, jolla on kohtuullista mielenkiintoa toimintaan. Tämä osuus harmaantuu ja puolittuu 20 vuodessa. Kysymys kuuluukin: onko meille jatkajia? Jos nykyinen trendi jatkuu tällaisenaan, vastaus lienee karu: ei.

Siksi olisikin olennaista saada nykyinen trendi murtumaan. Ja se voi tapahtua ainoastaan panostamalla nuoriin — jopa nuoriin, jotka eivät ole tässä kohtaa vielä syntyneet. Valitettavasti olen itse dataihminen, en ihmis-ihminen. Siksi en tiedä, miten trendin käytännössä saisi murtumaan. Omat lapseni olen saanut kasvatettua suuripiirtein kunnialla aikuisiksi, mutta ei minulla ole aavistustakaan miten nuoria tavoittaisi.

Mutta.

Joskus data saattaa antaa vihjettä positiivisestakin tarinasta. Seurakuntavaalien ehdokkaat eivät välttämättä ole kovin hyvä mittari sille, miten aktiivisia seurakuntalaiset ovat. Keräsin kuitenkin kaikkien Turun ja Kaarinan seurakuntayhtymän ehdokkaiden ikätiedot, ja alla nähdään mielenkiintoinen ilmiö. Ehdokkaiden keski-ikä on odotetusti korkea, 54 vuotta (mediaani on 56 vuotta). Alle 40-vuotiaita on vain kourallinen.

Jos tehdään sovitus 30 ja 75 ikävuoden välillä, saadaan punaisen viivan kaltainen trendi, jonka perusteella mielenkiinnon vielä nuoremmissa ikäryhmissä pitäisi mennä hyvin lähelle nollaa. Mutta käykin toisin: alle kolmekymppisiä ehdokkaita (punaisen katkoviivan kohdalla) onkin merkittävästi enemmän kuin mikään trendi antaisi ymmärtää.

Tämä on vain yksi datapiste, eikä kovin luotettava sellainen. On mahdollista, että seurakuntavaaleissa on aina ollut tällainen jakauma (dataa en ole löytänyt). Silti se antaa pienen vihjeen siitä, että jotain epäjatkuvuutta voisi olla. Ja tällaisessa tilanteessa, kun lineaarinen sovitus on synkähkö, mikä tahansa epäjatkuvuus herättää toivoa.

Tämä epäjatkuvuus on siis lupaava signaali, ja sitä pitää kehittää ja vaalia. Ensi valtuustokaudella juuri nuorten aktivoimisen pitää olla yksi tärkeimmistä tehtävistä seurakunnissa.

 

Työskenten ammatikseni datan kanssa, ja olen kiinnnostunut hallinnon koukeroista ja muista tylsistä asioista. Olen ehdolla Turun Katariinan seurakunnassa (numerot 19 & 71, vaalikonevastaukset) 

Tylsyys seurakunnan voimavarana

Minulla on supervoima. Innostun tylsistä asioista: numeroista, prosesseista, hallinnosta, budjeteista, strategioista, datasta.  Tylsyyttä ei lasketa perinteiseksi kristilliseksi armolahjaksi, mutta oikeastaan pitäisi.  Seurakunnan luottamushenkilön tärkein rooli on hoitaa tylsät tehtävät, jotta todelliset tähdet — eli työntekijät ja dynaamisemmat vapaaehtoiset —  pystyvät hoitamaan mielenkiintoiset tehtävänsä.

Olen ehdolla Turun Katariinan seurakuntavaaleissa (numerot 19 & 71, vaalikonevastaukset). Tämä kirjoitus julkaistu myös Turun Vihreän Kirkon blogissa 27.9.2022.

Olen ollut nyt yhden kauden tylsyyttä jalostamassa Katariinan seurakuntaneuvostossa. Lisäksi olen ollut neuvoston työjaostossa, jossa pienemmällä porukalla mm valmistellaan esityslistoja kokouksiin ja tehdään muutakin taustatyötä. Olen myös yhtymän yhteisessä tarkastusjohtokunnassa, joka yrittää ymmärtää miten yhtymä toimii. Uskon — tai ainakin toivon — että alan tätä kautta pikkuhiljaa hieman ymmärtämäänkin ainakin joistakin asioista edes jotain. Siksi haen jatkoa.

Luottamushenkilönä oleminen on oikeastaan minulle ainoa luonteva tapa palvella seurakuntaa. En laula. Inhoan väkijoukkoja. En halua hymyillä, jos ei hymyilytä. Ajatus siitä, että minun pitäisi rupatella rennosti vieraiden ihmisten kanssa ja puhua tunteista on…. no, Jean-Paul Sartre on kirjoittanut sellaisesta kokonaisen kirjan; sen nimi on Suljetut Ovet, ja se kertoo helvetistä.

Onneksi, onneksi, onneksi on ihmisiä jotka tuollaisesta pitävät. Heidän tukenaan haluaisin olla, taustalla, mahdollistamassa noita asioita. Kaikki hauska vaatii hallinnointia, ja sitä osaan. Leipätyökseni pyörittelen dataa ja pohdiskelen prosesseja. Mielelläni teen sitä vapaa-ajallakin.

En siis ole mikään perinteinen seurakunta-aktiivi. Taustani on kyllä hyvinkin kristillinen: olen lähetyslapsi, luterilaisuuuteen kasvanut ja saturoitunut papinpoika, ja lisäksi myös papin puoliso. Kuulun vahvasti kirkon liberaaliin siipeen, ja kannatan kaikkia Vihreän Kirkon teesejä (olenhan ollut niitä osaltani muotoilemassakin).

Liberaaliksi olen toisaalta aika pessimisti. En usko, että pystymme enää estämään katastrofaalista ilmastonmuutosta joka tärvelee lähes kaiken hyvän ja arvokkaan mitä olemme saaneet aikaan.  Kun se kriisi aikanaan iskee, tarvitaan profeetallisia tahoja jotka viimeiseen saakka puolustavat heikoimpia.

Jos tiivistän karusti, haluan pitää kirkon hengissä nykyisten hyvien aikojen yli, jotta se on käytettävissä kun todella kovat ajat koittavat. Hengissä pitäminen vaatii kahta asiaa: suuria muutoksia, ja toisaalta pieniä tavallisia asioita.

Esimerkiksi tasa-arvoasioissa kirkonkin on nyt tultava 2000-luvulle, jos se aikoo 2000-luvulla olla minkäänlainen toimija. Itse tunnen — ja arvostan — useita erittäin konservatiivisia kristittyjä, ja ymmärrän heidän tuskansa erityisesti avioliittoasiassa. Opillisesti se on vaikea asia. Mutta silti on löydettävä tapa edetä.

Pienet tavalliset asiat taas ovat paras tapa varmistaa, että ihmisillä ylipäätään säilyy mitään mielenkiintoa kirkkoa kohtaan.  Tällaisia asioita ovat Katariinassa esimerkiksi partio ja diakoniatyö. Tämä ei tarkoita sitä, että tehdään pelkästään sellaisia leppoisia asioita joita kaikki yksimielisesti kannattavat. Seurakunnalla tulisi olla aktiivinen ote esimerkiksi paperittomien auttamiseen, vaikka aihe ei kaikkia miellytäkään. Joskus on toimittava oikein, vaikka se herättäisi närää.

 

Maalaisjärki vai perehtyminen?

Erään puolueen paikallisosaston aluevaalisloganina on “Tervettä maalaisjärkeä”. Tämä kuulostaa maalaisjärjellä ajatellen hyvältä. Mutta saadaanko sillä kuitenkaan oikeasti parempia päätöksiä? Tarvitaanko aluevaltuuston päätöksenteossa arki-, maalais- tai kaupunkilaisjärkeä, vai olisiko kuitenkin viisaampaa perehtyä selvityksiin ja asioiden taustoihin? (Kirjoitus tehty yhdessä Kari Jakobssonin kanssa ja julkaistu tiedepuolue.fi-sivulla). 

Olemme voimakkaasti sitä mieltä, että perehtyminen on tärkein asia päätöksenteossa. Poliitikon ei tarvitse olla huippuälykäs tai huippukoulutettu. Sen sijaan hänen täytyy olla ahkera ja sinnikäs, ja jaksaa perehtyä, perehtyä ja perehtyä. Arkijärkeä tarvitaan, mutta hyvinvointialueilla päätetään erittäin suurista ja monimutkaisista kokonaisuuksista. Silloin mikään ei voi korvata kunnollisia selvityksiä.

Löysimme hyvän ja konkreettisen esimerkin Sanomien vaalikoneesta. Siinä on kysymys:  ”Nykyisin koululaisilla on kolme laajaa terveystarkastusta peruskoulun aikana. Määrää tulisi lisätä neljään, vaikka se lisäisi kustannuksia.” 

Kysymys on näennäisesti yksinkertainen, mutta oikeasti se avaa todellisen matopurkin uusia kysymyksiä.  Jakke vastasi siihen näin: ”Lisäisin ennemmin riskiperustaista seurantaa, eli tiivimpää seurantaa niille joilla on riskejä.” Karin vastaus taas oli  “”Määrän lisäämisen sijaan tulisi kehittää terveystarkastusten tasapuolista laatua ja parantaa yleistä koulujen terveyspalveluiden saatavuutta.”

Oikeastaan kumpikin meistä vastasi turhan poliitikkomaisesti. Oikein vastaus olisi jotakin tämänsuuntaista: “En tiedä. Haluan, että viranhaltijat selvittävät ajatuksen hyödyt ja haitat kunnolla läpi, jotta voimme tehdä päätöksen todelliseen tietoon pohjautuen”.

Jokaisessa päätöksessä on nimittäin sekä haittoja että hyötyjä. Pikaisesti ajateltuna lisätarkastuksista ei ajattelisi olevan mitään “haittaa”, mutta on niistä. Jos tarkastuksia lisätään 33%  (kolmesta kerrasta neljään), se 33% pitää löytää jostakin. Joko vähennetään kouluterveydenhoitajien (ja koululääkäreiden) muita töitä 33% edestä, tai sitten palkataan lisää henkilökuntaa 33% edestä.

Töiden vähentäminen tuskin tulee kyseeseen.  Kouluterveydenhoidolla oli ennen koronaakin haasteita ehtiä tekemään kaikki pakolliset tarkastukset, eikä tilanne todellakaan ole siitä korona-aikana parantunut.

Työntekijöiden lisääminen vaatii sinällään vain budjetin lisäämistä, mutta silloin on jo voitava kysyä, käytetäänkö tässä oikeasti rahaa mitenkään järkevällä tavalla. Jos oikeasti on varaa lisätä kalliisti koulutettujen terveydehoitajien ja lääkäreiden  määrää, eikö heidän osaamiselleen olisi huomattavasti järkevämpääkin käyttöä?

Työntekijöiden näkokulmasta jo työn mielekkyyttäkin voi pohtia. On vaikea nähdä, miksi juuri rutiininomaisten terveystarkastusten tehtailu vuodesta olisi se unelmatehtävä, jonka takia joku hakeutuu kouluterveydenhoitajaksi tai -lääkäriksi.

Toisaalta Jaken esittämä riskiperustainen testauskaan ei ole itsestäänselvästi hyvä asia. Liikutaan hyvin herkällä alueella. Jos osa oppilaista valitaan riskiperusteisesti tarkempaan seurantaan, miten “riski” määritellään? Tämä on itse asiassa suhteellisesti helpoin kysymys, koska sille löytyy kohtuullisen tarkkoja lääketieteellisiä perusteluja. Mitkään riskirajat eivät tietenkään ole koskaan aivan tarkkoja, vaan joku jää aina juuri riskirajan väärälle puolelle, vaikka oikeastaan tarvitsisi apua aivan yhtä paljon kuin juuri rajan toiselle puolelle päätynyt koululainen. Tämä on kuitenkin pystyttävä hyväksymään.

Paljon vaikeampi asia riskiperustaisuudessa on yksityisyydensuoja. Konkreettisimmalla tasolla: jos esimerkiksi ylipainoisia oppilaita alettaisiin seurata muita tarkemmin, miten pidetään huolta että muut lapset eivät huomaa tätä? On aivan todellinen riski joutua muiden lasten kiusaamaksi, jos joku “joutuu erityistarkkailuun”.

Yksilöllinen seuranta voi myös pahimmillaan johtaa vielä suurempiin ongelmiin kuin alkuperäinen riskitekijä.  Ylitarkka painon seuraaminen voi esimerkiksi altistaa syömishäiriöille, kehon kuvan häiriöille, tai jopa mielenterveyden ongelmille. Lisäksi seuraaminen ei hyödytä mitään, ellei ongelmiin ole myös keinoa puuttua. Jos koulu ei voi käytännössä tarjota kunnollisia työkaluja painonhallintaan, kannattaako sen edes seurata ylipainoa? Voiko esimerkiksi netissä oleva laadukas ravitsemus- ja painonhallintavalmennus korvata yksilöllistä valmennusta?

Vielä ylipainoakin suurempia riskejä voi tulla eteen, jos halutaan seurata asioita jotka eivät suoraan taivu numeroiksi, kuten esimerkiksi mielenterveyden ongelmia tai syrjäytymisriskiä. Jos jonkun lapsen todetaan jo alakouluikäisenä olevan syrjäytymisvaarassa, voiko tästä tulla itseään toteuttava ennuste, jos lapsi huomaa sen itsekin ja alkaa uskoa siihen?

Mikään näistä riskeistä ei välttämättä toteudu, mutta ne kaikki on otettava huomioon kun arvioidaan, mitä kannattaa lopulta tehdä. Jokainen saa vapaasti käyttää maalaisjärkeään omien lastensa kasvatuksessa.  Tilanne muuttuu täysin, jos pitää tehdä päätöksiä, jotka koskevat koko maakunnan kaikkia koululaisia. Silloin maalaisjärjellä saa helposti aikaan vain sutta ja sekundaa.

Terveystarkastuskysymykseen ei tässä kohtaa oikeastaan pitäisikään vastata juuta eikä jaata, vaan odottaa todellisia selvityksiä, perehtyä niihin, ja sitten vasta sanoa jotain. Suuri osa terveydenhuollon suurista kysymyksistä on juuri tämän tyyppisiä. Siksi sellainen aluevaltuutettu on viisain, joka myöntää miten vähän oikeasti tietää. Tietoa kyllä saa esimerkiksi viranhaltijoilta tai tutkijoilta, kun sitä vain osaa kysyä.

Jakke Mäkelä,  Dataintoilija ja fyysikko, Aluevaaliehdokas Varsinais-Suomessa (172)

Kari Jakobsson, Sosiaalitieteitä harrastuksena opiskeleva diplomi-insinööri,   Aluevaaliehdokas Varsinais-Suomessa (144)

Jakke Mäkelä: Olen fysiikan tohtori, toimin data-alalla, ja olen Varsinais-Suomen Vihreiden ehdokas tammikuun 2022 aluevaaleissa. Lisää tietoa aluevaaliteemoistani löydät täältä.

Translate »