Olen havahtunut siihen, että olen saattanut olla ylioptimistinen. Tunne on erikoinen.
Jottei tule epäselvyyttä: nykytiedoilla olen jämerästi “ilmastouskovainen”. Tiede ei tämän selvemmäksi voi tulla, ja olisi järjetöntä olla toimimatta vaikka epäselvyys olisi paljon suurempikin. Pidän kuitenkin samalla jämeryydellä kiinni siitä, että oma leirini ei saa käyttää huonoja argumentteja. Uskottavuutta ei saa menettää.
Aiemmassa kirjoituksessa avasin, miksi ilmastonmuutosta ei voi “ymmärtää”. Se on yksinkertaisesti liian monimutkainen kasa sairaita matemaattisia yhtälöitä, jotka eivät maalaisjärjellä kerta kaikkiaan avaudu. Lisäksi probabilistiset ennusteet antavat tietoa sellaisessa muodossa, jota terveet ihmisaivot eivät kykene absorboimaan.
Pahin unohtui. Ilmastonmuutoksen olemassaolo voidaan todistaa ennen muuta tilastoilla. Valitettavasti tilastoilla ei varsinaisesti voi todistaa mitään.
Tilastotieteen perusajatuksia on hypoteesin testaus. Esitetään väite (nollahypoteesi), ja sen jälkeen testataan, voidaanko osoittaa että väite on melko varmasti epätosi. Viime kädellä tilastoilla osoitetaan väitteitä vääriksi; se ei silti tarkoita, että vastakkainen väite olisi automaattisesti oikea. Jos tätä ei ymmärrä, popularisoinneissa voi mennä pahasti metsään.
Liian kansantajuisten mallien esittäminen jopa lyö itseään vastaan. Niissä on aina oiottu ja yksinkertaistettu, ja milloinkaan ne eivät vastaa todellisuutta kunnolla. Kun sitten jokin tällainen kansantajuinen malli osoittautuu virheelliseksi, vastapuoli saa tilaisuuden lytätä koko tutkimuksen. Olkinukkeargumentti, mutta ilmastouskova on itse luonut olkinukkensa.
Ilmastouskovan olisi parempi nöyrästi myöntää, että tulkinnoissa on epävarmuutta. Tapausesimerkkinä otan SkepticalSciencen sinällään mainion grafiikan.
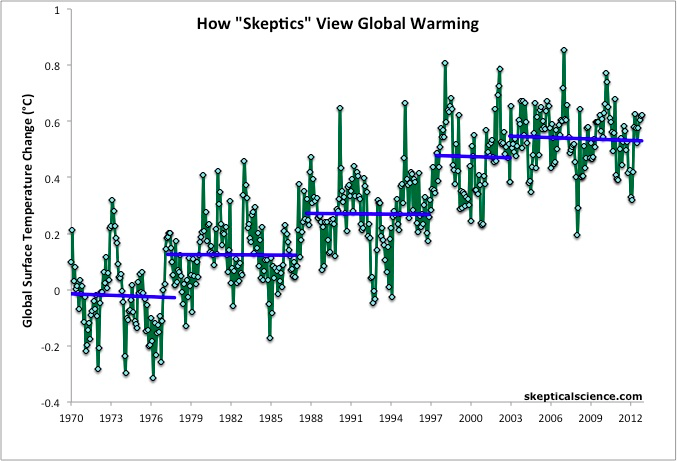

(Lähde: http://www.skepticalscience.com/graphics.php?g=47)
Grafiikan perusteellla “skeptikot” ovat kiinnittäneet huomiota siihen, että viimeisten 15 vuoden aikana keskilämpötila on laskenut. On se. Vuoden 1970 jälkeen on ollut peräti viisi viilenemisjaksoa… jos unohtaa sen että näiden jaksojen välissä lämpötila on yhdessä yössä noussut kymmeniä kertoja enemmän. Mitään fysikaalista järkeä tuollaisessa tulkinnassa ei ole.
Vastaavasti “realistit” tulkitsevat datan tavalla, joka ei vaadi fysiikan lakien vastaisisia ihmekuumenemisia. Sen tulkinnan mukaan lämpötilassa on paljon kohinaa, mutta koko ajan se on keskimäärin noussut.
Esitys on nokkela, kansainomainen ja näyttävä. Olen nähnyt sitä käytettävän myös suomalaisessa ympäristökeskustelussa. Valitettavasti on riski, että se voi kompastua omaan nokkeluuteensa.
Suoran viivan sovittaminen dataan nimittäin on helppoa mutta vaarallista — niin tehdään siksi että niin tehdään aina. Oikeasti lähes mihin tahansa dataan voi sovittaa lähes minkä tahansa käyrän. Ammattitaito syntyy siitä, että osaa poistaa ne käyrät jotka eivät kuvaa todellisuutta.
Yllä oleva kuvapari kyllä osoittaa sen, että “skeptikoiden” tulkinta on järjetön. Sen sijaan se ei kerro, onko “realistien” tulkinta oikea. Käytännössä tähän dataan voisi hyvin sovittaa myös käyrän, jonka kasvu alkaa pysähtyä noin vuoden 2000 tienoilla. Jopa niin, että jos saisin nämä datat eteeni tietämättä niistä mitään, aloittaisin kokeilun jollakin sellaisella epälineaarisella sovituksella.
Olenkin yrittänyt löytää raakadataa johon tuo sovitus on tehty, mutta en löytänyt. Käytin kuitenkin yhtä datasettiä joka on ollut tuossa taustalla, NOAA GSTA. Data kertoo poikkeaman pitkän aikavälin keskiarvosta. (Raakadata csv-formaatissa: NOAA. R-skriptit: NOAA.R)
Dataan saa mukavasti sovitettua suoran Y=-0.11+0.027*X, missä X on vuosia alkaen vuodesta 1970. Sovituksen R2-arvo on 0.53, mikä on säämittauksissa kohtuullinen joskaan ei loistava arvo. (R2=1 tarkoittaisi että datapisteet ovat käytännössä kaikki punaisella viivalla, R2=0 tarkoittaa että ne ovat missä sattuu).

Toisaalta dataan voi aivan yhtä hyvin sovittaa myös vaikkapa kolmannen asteen polynomin. Sen arvoksi tulee Y= -0.02 + 0.0026*T + 0.0014*T^2 – 0.000022*T^3. Tässä sovituksessa kasvu tosiaankin pysähtyy. Sovituksen R2-arvo on lähes täsmälleen sama kuin lineaarisen, eli ei ole mitään varsinaista syytä pitää sitä huonompana.

Dataan voi myös sovittaa kosinifunktion (miksi ei voisi?). Sovitus ei ole aivan yhtä täydellinen kuin kahdessa edellisessä, mutta R2-arvo on silti 0.51 jos käytetään sovitusta Y= 0.41 – 0.45* cos(Y*π/36)). Tämä yksinkertaisesti tarkoittaisi, että lämpötilaa ajaa noin 144 vuoden pituinen sykli.

Olisi mukavaa sanoa, että nämä sovitukset ovat naurettavia, mutta tilastomielessä ne eivät ole. Jos kaksi sovitusta antaa käytännössä yhtä hyvän tuloksen, on vaikea mennä väittämään toista paremmaksi. (Jokainen näistä sovituksista muuttuu, jos mennään ajassa kauemmas taaksepäin. Mutta millä tahansa ajanjaksolla katsottuna suora viiva ei yleensä ole erityisen hyvä kuvaaja).
Itse asiassa nämä sovitukset eivät välttämättä edes ole naurettavia, ei edes tuo kosinisovitus. Epälineaarisuus voi jopa olla todellista, ja perustua oikean fysiikkaan. Se vaikuttaa hämärältä vain, jos ei ymmärrä eroa “lämpötilan” ja “energian” välillä.
Ilmakehään ei tällä hetkellä pumpata liikaa “lämpötilaa”; siihen pumpataan liika energiaa. Ero on merkittävä. Energia voi siirtyä moneen eri paikkaan: esimerkiksi syvälle mereen, tai jäätiköiden sulattamiseen, tai yläilmakehään. Silloin se ei lämmitä maanpintaa. Mutta jos “ylilämpö” voi siirtyä yllättävästi, se voi myös palata yllättävästi.
Yhden ainoan pintalämpötilan seuraaminen ei siis kerta kaikkiaan kerro koko totuutta. Tilastoja väärinkäyttämällä voidaan “todistaa” oikeastaan mitä vain. Toisaalta tiedetään, että malleissa on otettava huomioon muitakin muuttujia kuin pintalämpötila, eikä kaikkia ilmiöitä edelleenkään osata asteen tarkkuuudella mallintaa.
Tilastoja on syytä käyttää varovasti, ellei tiedä täsmälleen mitä on tekemässä.
Lisää kirjoituksia ympäristöstä: täällä.
Like this:
Like Loading...













